应用数学学报

Select

1. 磁盘发电机系统的动力学研究及其在混沌同步中的应用

张付臣, 舒永录, 姚宪忠

应用数学学报 2013, 36 (2): 193-203. DOI: 10.12387/C2013016

摘要（883）

PDF（pc）（537KB）（1551）

本文通过构造适当的Lyapunov函数, 研究了磁盘发电机系统的最终有界集、正向不变集和全局指数吸引集, 得到了该系统界的四维椭球估计表达式. 然后将所得到的该系统界的估计应用到完全同步之中去, 并做出了相应的数值模拟.

参考文献 | 相关文章 | 多维度评价

Select

2. n-double图的连通性

郭利涛, 覃城阜, 郭晓峰

应用数学学报 2013, 36 (2): 204-208. DOI: 10.12387/C2013017

摘要（834）

PDF（pc）（226KB）（1192）

设G₁=(V₁, E₁), G₂=(V₂, E₂)是两个连通图, 直积(direct product) (也称为Kronecker product, tensor product 和cross product) G₁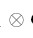

G₂ 的点集为 V(G₁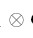

G₂) = V(G₁)

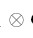V(G₂), 边集为E(G₁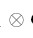

G₂) = {(u₁, v₁)(u₂, v₂): u₁u₂ ∈ E(G₁), v₁v₂ ∈E(G₂)}. 简单图G的 n-double图D_n[G] = G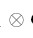

T_n,其中n个点的全关系图 T_n是完全图K_n在每个点加上一个自环得到的图. 在本文中, 我们研究了D_n[G] 的(边)连通性, 超(边)连通性.

参考文献 | 相关文章 | 多维度评价

Select

3. 超级限制边连通二部图的充分条件

刘爱霞, 原军

应用数学学报 2013, 36 (2): 209-216. DOI: 10.12387/C2013018

摘要（943）

PDF（pc）（303KB）（1788）

设S是连通图G的一个边割. 若G-S不包含孤立点,则称S是G的一个限制边割. 图G的最小限制边割的边数称为G的限制边连通度,记为λ'(G). 如果图G的限制边连通度等于其最小边度,则称图G是最优限制边连通的,简称λ'-最优的. 进一步,如果图G的每个最小限制边割恰好分离出图G的一条边,则称图G是超级限制边连通的,简称超级-λ'的. 设G是一个最小度δ(G)≥2的n≥4阶二部图,ξ(G)是G的最小边度. 本文证明了(a) 若ξ(G)≥((n/2)-2)(1+1/(δ(G)-1)), 则G是λ'-最优的;(b) 若ξ(G)>(n/2)-2)(1+1/(δ(G)-1)), 则G是超级-λ'的,除非图G是K_2,n-2, n≥ 6 或是Cartesian积图 K_n/4,n/4×K₂, 其中n≥8 且n整除4. 最后,论文举例说明该结果是最好可能的.

参考文献 | 相关文章 | 多维度评价

Select

4. 有重复观测的变系数EV模型的参数估计

李泽华, 刘金山, 吴小腊

应用数学学报 2013, 36 (2): 217-229. DOI: 10.12387/C2013019

摘要（1123）

PDF（pc）（370KB）（1508）

构造了有重复观测的变系数EV模型中的诸多参数估计, 包括系数函数、测量误差方差以及测量误差与回归误差的协方差等估计, 去除了有关测量误差方差已知或可靠比已知的假定. 在一些较弱的条件下, 证明了所有的这些估计都是强相合的, 同时获得了系数函数估计的渐近正态性以及收敛速度.

参考文献 | 相关文章 | 多维度评价

Select

5. 一类具有交叉扩散的捕食模型非常数正解的存在性

李艳玲, 李景荣, 郭改慧

应用数学学报 2013, 36 (2): 230-242. DOI: 10.12387/C2013020

摘要（865）

PDF（pc）（348KB）（1260）

研究了一类具有扩散和交叉扩散项的Holling-Tanner捕食-食饵模型. 首先利用最大值原理和Harnack不等式给出正解的先验估计, 进一步利用度理论得到非常数正解的存在性与不存在性, 从而给出非常数正解存在的充分条件.

参考文献 | 相关文章 | 多维度评价

Select

6. 各向异性板半无限裂纹平面问题的保角变换解法

贾红刚, 聂玉峰

应用数学学报 2013, 36 (2): 243-248. DOI: 10.12387/C2013021

摘要（985）

PDF（pc）（298KB）（1347）

本文给出了各向异性板半无限裂纹平面问题的保角变换解. 首先, 简单介绍了各向异性板平面问题的基本理论. 随后采用复变函数的方法, 通过引用适当的保角映射研究了各向异性板半无限裂纹平面弹性问题, 得到了各向异性板中半无限裂纹在任意面内集中载荷作用下的裂纹尖端的应力强度因子的解析解. 最后,作为特例得到了当集中力作用在裂纹表面时的应力强度因子的解析解,依此验证了结果的正确性. 结果表明该方法简单实用.

参考文献 | 相关文章 | 多维度评价

Select

7. Banach空间中脉冲微分方程初值问题解的存在性

秦丽娟

应用数学学报 2013, 36 (2): 249-256. DOI: 10.12387/C2013022

摘要（880）

PDF（pc）（278KB）（1498）

利用凝聚映射的不动点定理, 对脉冲函数不加紧性条件和其他额外条件, 通过逐段延拓的方法, 获得了无穷区间上脉冲微分方程初值问题解的存在性, 本质上改进了某些已知的结果.

参考文献 | 相关文章 | 多维度评价

Select

8. 新型广义加权保费原理下风险保费的信度估计

温利民, 梅国平

应用数学学报 2013, 36 (2): 257-268. DOI: 10.12387/C2013023

摘要（1041）

PDF（pc）（411KB）（1431）

本文研究了新型广义加权保费原理下风险保费的信度估计问题. 利用了损失函数法, 将新型广义加权保费原理定义为新型广义加权损失函数下风险的最优估计. 在该损失函数下, 把估计限定在经验估计的线性组合, 根据均方误差最小原则得到风险保费的信度估计, 并证明了信度估计的相合性. 最后, 在 Esscher保费原理下对信度估计的相合性进行模拟验证, 并在指数保费原理下与前人的结果进行了比较, 结果发现已有的研究只是本文的一种特殊情况.

参考文献 | 相关文章 | 多维度评价

Select

9. Dirichlet函数类的Fejér算子逼近

陈英伟, 王志军, 王占京

应用数学学报 2013, 36 (2): 269-279. DOI: 10.12387/C2013024

摘要（969）

PDF（pc）（266KB）（1183）

对Cⁿ中的单位球B_n上的Dirichlet类D_p, 得到与Hardy空间H^p的包含关系, 并获得其精确的多项式逼近阶和以Hardy空间度量的Fejér算子逼近的一个上界估计.

参考文献 | 相关文章 | 多维度评价

Select

10. 最大度为8不含特定子图的平面图的全染色

蔡建生, 王光辉, 闫桂英

应用数学学报 2013, 36 (2): 280-292. DOI: 10.12387/C2013025

摘要（1064）

PDF（pc）（365KB）（1334）

全染色是对图G的顶点和边同时进行正常染色, 至少要用Δ+1个色才能对图G进行正常全染色. 本文运用权转移的方法, 证明了最大度为8的不含特定子图的简单平面图是9-全可染的.

参考文献 | 相关文章 | 多维度评价

Select

11. 轴突输运中的行波解

黄艳, 李杏

应用数学学报 2013, 36 (2): 293-297. DOI: 10.12387/C2013026

摘要（881）

PDF（pc）（218KB）（1294）

本文对于起源于神经科学的一类轴突输运方程研究了行波解的性质,从数学上解析了神经信号是如何通过行波解传递的.

参考文献 | 相关文章 | 多维度评价

Select

12. 一类非线性斯图谟-刘维尔方程两点边值问题解的存在性

陈健, 沈娟, 王其申

应用数学学报 2013, 36 (2): 298-305. DOI: 10.12387/C2013027

摘要（911）

PDF（pc）（285KB）（1090）

本文讨论了如下非线性斯图谟-刘维尔方程的第一边值问题

解的存在性, 其中p(x)在区间[0,1]上是x的分段常数.

参考文献 | 相关文章 | 多维度评价

Select

13. 一类带非线性无穷大边界值条件的二阶半线性方程奇摄动问题

胡永生, 沈建和, 周哲彦

应用数学学报 2013, 36 (2): 306-314. DOI: 10.12387/C2013028

摘要（865）

PDF（pc）（357KB）（1303）

研究了一类带非线性无穷大边界值条件的二阶半线性方程的奇摄动边值问题. 利用边界层函数法, 分别构造了左、右边界层的校正函数(含指数型和代数型), 得到了奇摄动问题解的渐近行为; 根据微分不等式理论, 证明了该问题解的存在性, 并给出了退化解与精确解的误差估计. 通过与数值积分解进行比较, 一个典型的算例验证了本文理论结果的正确性.

参考文献 | 相关文章 | 多维度评价

Select

14. 高阶非线性奇摄动微分方程的三点边值问题

丁海云, 倪明康

应用数学学报 2013, 36 (2): 315-323. DOI: 10.12387/C2013029

摘要（822）

PDF（pc）（330KB）（1220）

本文讨论了一类高阶非线性奇摄动微分方程的三点边值问题. 根据小参数的不同次幂, 分情况补充相应的边界条件. 运用边界层函数法, 构造了形式渐近解, 并得到解的存在唯一性和渐近解的一致有效性. 最后用数值计算结果印证了结论.

参考文献 | 相关文章 | 多维度评价

Select

15. Banach空间中关于变分不等式组与严格伪压缩映射的粘滞逼近法

刘英

应用数学学报 2013, 36 (2): 324-336. DOI: 10.12387/C2013030

摘要（1123）

PDF（pc）（305KB）（1118）

本文利用粘滞逼近法建立了一迭代序列来逼近两个集合的公共元素, 这两个集合分别是Banach空间中广义变分不等式组的解集与Banach空间中有限个严格伪压缩映射的公共不动点集. 本文证明了该迭代序列强收敛到这两个集合的某一公共元素, 且该元素为某一变分不等式的解.本文的结果提高与推广了许多相关结论.

参考文献 | 相关文章 | 多维度评价

Select

16. 二维非饱和土壤水分运动方程的径向基配点差分法

苏李君, 王全九, 秦新强, 曾辰

应用数学学报 2013, 36 (2): 337-349. DOI: 10.12387/C2013031

摘要（29）

PDF（pc）（1132KB）（1054）

针对二维非饱和土壤水分运动方程, 将径向基配点法结合差分法构造了一种新的数值算法。该算法先采用差分法处理非线性项, 再利用径向基函数配点法的隐格式求解方程, 避免了因非线性项的存在导致不能直接使用配点法的现象, 并且证明了该算法解的存在唯一性。通过对非饱和土壤水分运动的数值模拟, 并采用试验数据对新算法进行了验证, 模拟结果与试验结果非常吻合, 表明该算法实用、有效。同时, 比较分析了不同径向基函数以及不同算法的模拟精度, 结果表明, 与MQ函数和Guass函数相比, 新的径向基函数具有更好的模拟精度, 且相对于有限差分法和有限元法, 本文提出的方法具有一定的优越性.

相关文章 | 多维度评价

Select

17. 循环图C(9,2)与路P_n的笛卡尔积的交叉数

袁梓瀚, 黄元秋, 刘金旺

应用数学学报 2013, 36 (2): 350-362. DOI: 10.12387/C2013032

摘要（1031）

PDF（pc）（423KB）（1371）

C(m,2)表示由圈C_m (v₁v₂…v_mv₁)增加边 v_iv_i+2 (i=1,…,m,i+2 (mod m))所得的循环图. C(m,2)的一点悬挂(两点悬挂)是增加一个顶点x (两个顶点x,y)和边xv (边xv, yv)的图, 其中v∈ V(C(m,2)). 我们证明了9阶循环图C(9,2)与路P_n的笛卡儿积的交叉数是10n; C(2m-1,2)的一点悬挂和两点悬挂的交叉数分别是m,2m.

参考文献 | 相关文章 | 多维度评价

Select

18. 时标上二阶带p-Laplacian算子的脉冲边值问题单调迭代正解的存在性

杨军, 娜娜, 金燕

应用数学学报 2013, 36 (2): 363-375. DOI: 10.12387/C2013033

摘要（995）

PDF（pc）（288KB）（902）

论文利用单调迭代的方法证明了时标上二阶带p-Laplacian算子的脉冲边值问题的正解存在性. 同时, 举例阐述了主要结果.

参考文献 | 相关文章 | 多维度评价

Select

19. 一类分布鲁棒优化问题的线性化方法及其应用

纪颖, 李一军, 芦鹏宇, 周勇

应用数学学报 2013, 36 (2): 376-384. DOI: 10.12387/C2013034

摘要（1535）

PDF（pc）（370KB）（1141）

本文考虑一类特殊的极大极小化问题, 即分布鲁棒优化问题. 这类优化方法是不同于随机规划和鲁棒优化的一类方法, 在这类问题中, 不确定变量的概率分布往往是不能精确得知的, 只知道概率分布所满足的一些条件, 比如一次信息、二次信息以及支撑集合信息等. 如此分布鲁棒优化问题便是寻求在所有满足条件的分布中找寻满足最坏可能分布的解. 一般情况下, 这类优化问题的求解都是NP难的. 本文考虑一类简单的情形, 即考虑不确定变量的概率分布只满足一次信息、支撑集合信息以及仿射一次信息, 通过应用半无限规划问题的对偶性, 本文指出这类分布鲁棒优化问题等价于线性规划问题, 从而原分布鲁棒优化问题可以应用现成的求解线性规划的方法进行求解. 为验证方法的有效性, 本文将新方法应用于解决不确定条件下含有交易费用的利率管理问题.

参考文献 | 相关文章 | 多维度评价

Select

20. 广义矩阵分布下多元回归模型的贝叶斯推断

刘金山, 夏强, 黄香

应用数学学报 2013, 36 (3): 385-398. DOI: 10.12387/C2013035

摘要（1516）

PDF（pc）（359KB）（1627）

考虑具有奇异矩阵椭球等高分布误差的多元线性回归模型的贝叶斯统计推断,在非信息先验下得到了系数矩阵关于Hausdorff测度的后验边缘分布和未来观察值的预测分布,并得到了一类特殊奇异矩阵椭球等高分布下误差协方差矩阵的后验边缘分布.对于具有奇异矩阵正态分布误差的多元线性回归模型,在广义正态-逆Wishart共轭先验下得到了类似的后验边缘分布和预测分布结果.在上述两种先验分布下,回归系数矩阵的后验边缘分布和预测分布是双奇异矩阵t分布,这种分布具有关于Hausdorff测度的精确密度.结果表明,在非信息先验下,回归系数矩阵的后验边缘分布和未来观察值的预测分布在奇异矩阵椭球等高分布类中具有稳健性.

参考文献 | 相关文章 | 多维度评价

Select

21. 具有2ⁿ线性复杂度的2ⁿ周期二元序列的3错线性复杂度

周建钦

应用数学学报 2013, 36 (3): 399-413. DOI: 10.12387/C2013036

摘要（911）

PDF（pc）（334KB）（1579）

线性复杂度和k错线性复杂度是度量密钥流序列的密码强度的重要指标.通过研究周期为2ⁿ的二元序列线性复杂度,提出将k错线性复杂度的计算转化为求Hamming重量最小的错误序列.基于Games-Chan算法,讨论了线性复杂度为2ⁿ的2ⁿ周期二元序列的3错线性复杂度分布情况;给出了对应k错线性复杂度序列的完整计数公式,k=3,4.对于一般的线性复杂度为2ⁿ-m的2ⁿ周期二元序列,也可以使用该方法给出对应k错线性复杂度序列的计数公式.

参考文献 | 相关文章 | 多维度评价

Select

22. 一维p-Laplace二阶脉冲微分方程的奇异边值问题

魏君, 蒋达清, 祖力

应用数学学报 2013, 36 (3): 414-430. DOI: 10.12387/C2013037

摘要（1048）

PDF（pc）（335KB）（1439）

脉冲现象作为一种瞬时突变现象,在现代科技各领域的实际问题中是普遍存在的.本文研究具有奇异边值的一维p-Laplace二阶微分方程在脉冲影响下的正解的存在性,介绍了解的一般性存在定理,并用A-A定理和不动点定理证明了一维p-Laplace二阶脉冲微分方程的奇异边值问题的正解存在性定理.

参考文献 | 相关文章 | 多维度评价

Select

23. 具有中间亏指数的线性哈密顿算子的点谱

郑召文, 胡玉峰

应用数学学报 2013, 36 (3): 431-438. DOI: 10.12387/C2013038

摘要（917）

PDF（pc）（305KB）（1417）

本文讨论具有任意亏指数d的自伴线性哈密顿算子点谱与对应的线性哈密顿系统的平方可积解之间的关系.若对于某个实开区间中的任意点λ,系统总有d个线性无关解,则它的任何自伴算子的点谱在这个开区间上是不稠密的.

参考文献 | 相关文章 | 多维度评价

Select

24. 变动控制结构下几乎-锥-凸映射的标量函数刻画

余国林, 刘三阳

应用数学学报 2013, 36 (3): 439-447. DOI: 10.12387/C2013039

摘要（936）

PDF（pc）（269KB）（1280）

本文讨论变动控制结构下广义锥凸映射的线性和非线性标量函数的刻画问题.首先在变动序拓扑向量空间中证明了由正极锥的极方向所刻画的向量值映射的几乎-锥-凸性;其次,对变动控制结构引入了一种非线性标量函数,并利用这种非线性标量函数,得到了几乎-锥-凸向量值映射的标量刻画.

参考文献 | 相关文章 | 多维度评价

Select

25. WZ方法与一个二项式级数的部分和公式

陈奕俊

应用数学学报 2013, 36 (3): 448-453. DOI: 10.12387/C2013040

摘要（1122）

PDF（pc）（200KB）（1171）

本文基于WZ理论给出了Peter Paule与Carsten Schneider的一篇文章中的一个二项式级数的部分和公式的新证明,并且发现他们的文章中所给的另一个二项式级数的部分和公式实际上是错误的,我们给出了其相应的一个正确公式.

参考文献 | 相关文章 | 多维度评价

Select

26. 度量凸空间中Lipschitz型非自映射族的唯一公共不动点

朴勇杰

应用数学学报 2013, 36 (3): 454-462. DOI: 10.12387/C2013041

摘要（1000）

PDF（pc）（282KB）（1237）

考察了完备的度量凸空间框架下满足具有变系数的Lipschitz条件的非自映射族并根据给定的边界条件和映射族构造了一个收敛序列{x_n},然后证明了该序列的唯一极限正是映射族的唯一的公共不动点.最后给出了更广泛的结果.所得结果推广和改进了许多压缩型映射族的公共不动点定理.

参考文献 | 相关文章 | 多维度评价

Select

27. 加边与删边运算下图的亏格分布

郭婷, 黄元秋

应用数学学报 2013, 36 (3): 463-470. DOI: 10.12387/C2013042

摘要（1125）

PDF（pc）（333KB）（1373）

设(G,u,v)是以u和v为根的双根连通图,用边e连接点u和v,所得之图记为G+e.Gross对根u和v的度均为2的情形,给出了G+e的亏格分布与(G,u,v)的部分亏格分布之间的一个关系.本文推广到有一个根的度可以任意大的情形,并由(G,u,v)的部分亏格分布导出了G+e的亏格分布.

参考文献 | 相关文章 | 多维度评价

Select

28. 基于R-模的线性网络码

章照止, 姜楠

应用数学学报 2013, 36 (3): 471-479. DOI: 10.12387/C2013043

摘要（890）

PDF（pc）（355KB）（1118）

一般来讲,线性网络码是基于有限域的.本文的目的是要把基于有限域的线性网络码从理论上推广到基于一般R-模的线性网络码,其中R是一个给定的环.一类重要的R-模是Z-模,最简单的特例是整数环Z.另一大类重要的R-模是一般包含一个给定子环R的数域或代数数域的线性网络码.例如整数环Z有理数域Q实数域R复数域C.推广后网络传送的消息(信号)可以是实数或复数,因此扩大了应用的领域.

参考文献 | 相关文章 | 多维度评价

Select

29. 时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性

孙一冰, 韩振来, 孙书荣, 张超

应用数学学报 2013, 36 (3): 480-494. DOI: 10.12387/C2013044

摘要（977）

PDF（pc）（341KB）（1573）

借助时间尺度的有关理论,运用Riccati变换技巧,平均函数技术及不等式技巧,研究了时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性,给出该类方程振动的几个充分条件,推广并改进了已有的某些结果.

参考文献 | 相关文章 | 多维度评价

Select

30. Weibull分布步进应力加速寿命试验的Bayes估计

武东, 汤银才

应用数学学报 2013, 36 (3): 495-501. DOI: 10.12387/C2013045

摘要（1157）

PDF（pc）（347KB）（1373）

本文研究了定时和定数截尾情形CE模型下Weibull分布场合步进应力加速寿命试验的Bayes估计.利用加速系数和加速方程将各种加速应力水平下的尺度参数换算为正常应力水平下的尺度参数,从而获得含正常应力下尺度参数的似然函数.在参数先验的选取时,尺度参数和加速系数分别取共轭先验和无信息先验,当形状参数m<1和m>1时分别取Beta分布和Gamma分布作为其先验.在平方损失下,利用Gibbs抽样和切片抽样给出了该模型参数的Bayes估计.最后,通过Monte Carlo模拟表明该Bayes估计是有效的.

参考文献 | 相关文章 | 多维度评价

Select

31. 一类具有奇异性与真空的非牛顿流局部强解的爆破准则

方莉, 宋红丽, 郭真华

应用数学学报 2013, 36 (3): 502-515. DOI: 10.12387/C2013046

摘要（1011）

PDF（pc）（343KB）（1151）

探讨了如下一类非牛顿流

其初边值条件为

.
利用迭代方法,讨论了该模型的局部强解的爆破准则,证明了:如果T_*是强解(ρ,u)存在的最大时间且T_*<T₁,则

.

参考文献 | 相关文章 | 多维度评价

Select

32. 一类完全三部图的K_1,3-因子大集

郝国辉, 康庆德

应用数学学报 2013, 36 (3): 516-520. DOI: 10.12387/C2013047

摘要（1121）

PDF（pc）（253KB）（1424）

令G是一个有限图,H是G的一个子图.若V(H)=V(G),则称H为G的生成子图.图G的一个λ重F-因子,记为S_λ(F,G),是G的一个生成子图且可分拆为若干与F同构的子图(称为F-区组)的并,使得V(G)中的每一个顶点恰出现在λ个F-区组中.一个图G的λ重F-因子大集,记为LS_λ(F,G),是G中所有与F同构的子图的一个分拆{B_i}_i,使得每个B_i均构成一个S_λ(F,G).当λ=1时,λ可省略不写.本文中,我们证明了当v≡4mod24时,存在LS(K_1,3,K_v,v,v).

参考文献 | 相关文章 | 多维度评价

Select

33. 具S-型分布时滞的细胞神经网络的概周期解

周辉, 周宗福

应用数学学报 2013, 36 (3): 521-531. DOI: 10.12387/C2013048

摘要（1169）

PDF（pc）（348KB）（1387）

该文研究一类具S-型分布时滞的细胞神经网络(CNN_S)的概周期解及全局指数型稳定性问题.利用指数型二分性和Schauder不动点定理以及构造Lyapunov函数,得到了细胞神经网络模型概周期解和指数稳定性的一些充分条件.此外,给出一个实例说明结果是可行的.

参考文献 | 相关文章 | 多维度评价

Select

34. 点群6一维六方准晶狭长体中有限长Griffith裂纹的反平面问题

施志昱, 刘官厅

应用数学学报 2013, 36 (3): 532-540. DOI: 10.12387/C2013049

摘要（930）

PDF（pc）（402KB）（1331）

利用复变函数法,通过构造新的保角变换,研究了裂纹面受剪切作用下点群6一维六方准晶狭长体中有限长Griffith裂纹的断裂行为,得到了裂纹尖端处应力强度因子的解析解.当狭长体高度趋于无穷时,该解析解退化为无限大点群6一维六方准晶中有限长Griffith裂纹问题的解.

参考文献 | 相关文章 | 多维度评价

Select

35. 具有脉冲积分条件的一次脉冲积分-微分方程混合系统

胡兵, 乔元华

应用数学学报 2013, 36 (3): 541-552. DOI: 10.12387/C2013050

摘要（943）

PDF（pc）（281KB）（1352）

本文讨论具有脉冲积分条件的脉冲积分-微分方程混合类型的极值解的存在性.主要工具是上下解和单调迭代技术.

参考文献 | 相关文章 | 多维度评价

Select

36. {1,4,5}自相似集的摄动和强分离参数集

奚李峰, 戴美凤, 刘正慈, 刘云志

应用数学学报 2013, 36 (3): 553-565. DOI: 10.12387/C2013051

摘要（1049）

PDF（pc）（441KB）（1440）

对于自相似集E_λ=E_λ/5∪(E_λ/5+λ/5)∪(E_λ/5+4/5),本文讨论了λ靠近3(对应于{1,4,5}集)时,E_λ的维数逼近性质,强分离性,Lipschitz等价性等.此外,还探讨了参数集λ:E_λ不满足强分离条件}的几何结构.

参考文献 | 相关文章 | 多维度评价

Select

37. 二阶非线性时滞微分方程的多个正解

汪会民, 孟祥旺, 蒋威

应用数学学报 2013, 36 (3): 566-572. DOI: 10.12387/C2013052

摘要（1142）

PDF（pc）（239KB）（1392）

在这篇文章中,我们探讨了非线性边值问题正解的存在性.给出的主要结果证明了边值问题两个正解的存在性.结论的证明使用了一个锥上的不动点定理.为了说明定理的正确性,我们最后给出了一个例子.

参考文献 | 相关文章 | 多维度评价

Select

38. 两个旋转球之间粘性不可压缩流动的Lorenz系统

于佳平, 李开泰

应用数学学报 2013, 36 (4): 577-618. DOI: 10.12387/C2013053

摘要（1148）

PDF（pc）（3864KB）（4085）

两个不同角速度旋转球之间粘性流动问题是地球外部大气流动的简化模型. 通过引入球Bessel函数的有理表达式, 得到Stokes算子特征值与特征函数的有理表达形式. 利用Stokes算子特征函数作为基函数系, 对两个旋转球间流动问题进行谱Galerkin逼近. 由三模态的Glerkin逼近方程得到一个类Lorenz系统, 我们对此系统进行分歧问题和吸引子的讨论, 从而得到原问题的稳定性判定.

参考文献 | 相关文章 | 多维度评价

Select

39. 半定矩阵秩极小的非凸精确松弛

秦林霞, 修乃华, 孔令臣

应用数学学报 2013, 36 (4): 619-630. DOI: 10.12387/C2013054

摘要（1328）

PDF（pc）（381KB）（2122）

本文主要研究半定矩阵秩极小问题(P) 的非凸精确松弛及其性质. 首先, 为求解问题(P), 我们引入其Schatten p-范数(0<p<1) 松弛, 记为(S_p). 其次, 通过定义半定限制等距常数和半定限制正交常数, 我们给出了问题(P)有唯一解的充分条件. 最后, 利用半定限制等距性质, 我们给出了问题(P)和(S_p) 有相同唯一解的充分条件. 特别地, 对任意0<p<1, 我们还得到一个一致的精确恢复条件.

参考文献 | 相关文章 | 多维度评价

Select

40. 极大多线性Bochner-Riesz算子的Morrey空间估计

朱诗红

应用数学学报 2013, 36 (4): 631-639. DOI: 10.12387/C2013055

摘要（989）

PDF（pc）（215KB）（1557）

本文用分数次极大算子控制的方法,得到了极大多线性Bochner-Riesz算子在Morrey空间的有界性, 并且证明了它也是从M^{p₁,1+p₁(λ-β/n)}空间到BMO^λ,p₂空间上的有界算子，其中 1/p₁-β/n=1/p₂, -1/p₂≤λ<1/n.

参考文献 | 相关文章 | 多维度评价

应用数学学报 2013年 36卷

扫码分享