2017年, 第40卷, 第5期　刊出日期：2017-10-28

  

• 全选
  |

论文
• Select
  求解多集分裂可行问题的一种新的松弛投影算法

  张艳君, 赵金玲, 徐尔

  应用数学学报. 2017, 40(5): 641-652. https://doi.org/10.12387/C2017053

  摘要 ( ) PDF全文 ( )   可视化   收藏

  本文提出了求解多集分裂可行问题（Multiple-sets Split Feasibility Problem，简称MSFP）的一种新的松弛投影算法.已有求解MSFP的算法大多采用邻近函数p（x）：=（1/2α_i||x-P_Ci（x）||²+（1/2λ_j||Ax-P_Qj（Ax）||²度量点到所有集合的距离并在迭代中直接利用其梯度方向，与此不同，本文引入了新的搜索方向，并基于此提出了新的算法.搜索方向的不同导致了算法的收敛性证明上的明显差异.初步的数值计算结果表明新算法对于不同的问题都能够有较快的收敛速度，且在问题维数增大时表现得越发明显.

• Select
  生产状态转移对代理人问题和公司投资的影响

  王莹, 黄文礼, 杨晨, 李胜宏, 郑大厚

  应用数学学报. 2017, 40(5): 653-666. https://doi.org/10.12387/C2017054

  摘要 ( ) PDF全文 ( )   可视化   收藏

  在委托代理理论框架下，本文考虑更符合实际的市场环境，研究生产状态转换和重大损失风险两大不稳定因素对代理人贴现价值，公司价值及投资量的影响.文章根据最优合约理论和随机控制原理，在代理人与投资者之间建立一个动态最优合约模型，该模型一方面对代理人具有足够的激励作用，另一方面最大化投资者的价值函数.此外，延缓支付，清算风险和由生产状态转移引起的代理人报酬的补偿报酬等因素也都包含其中.文章发现：重大事故风险对高生产状态下投资量的影响大于对代低生产状态下投资量的影响.这一结果有效解释了行为经济学中当经理人面临清算时，在市场低迷状态下往往选择奋力一搏增加投资量，而在市场繁荣状态下的选择却更保守这一现象.其次，当不受代理人控制的生产状态转换发生时，代理人所得到的补偿价值对代理人具有重要的激励作用，但随着代理人价值函数的增加，激励作用逐渐减弱.该结论打破了代理人所得报酬应只与自身的表现有关，而不应受其他外界因素的影响这一传统认知；最后，投资决策依赖于公司效益，生产状态转换和清算风险也间接影响公司的投资决策.当生产状态好转时，且贴现价值的激励作用使代理人问题得到缓解，投资也变得更加有利，投资量会增加；反之亦然.
• Select
  具有正负系数的二阶中立型时滞Emden-Fowler方程的振动准则

  罗红英, 屈英, 俞元洪

  应用数学学报. 2017, 40(5): 667-675. https://doi.org/10.12387/C2017055

  摘要 ( ) PDF全文 ( )   可视化   收藏

  该文建立了具有正负系数的二阶中立型时滞Emden-Fowler方程（a（t）[x（t）+p（t）f（x（δ（t）））]'）+q（t）g（φ（x（σ（t））））-r（t）h（φ（x（t-τ）））=0，t≥t₀.的一切解振动的若干新的充分条件，所得结果改进和推广了已知的一些结论，我们也用例子来说明结果的意义.
• Select
  具有不同时滞的两种捕食者-食饵恒化器模型的定性分析

  孔丽丽, 李录苹

  应用数学学报. 2017, 40(5): 676-691. https://doi.org/10.12387/C2017056

  摘要 ( ) PDF全文 ( )   可视化   收藏

  研究了一类具有不同时滞和Monod型功能反应函数的两种捕食者-食饵恒化器模型.利用特征方程理论和比较定理，得到了系统平衡点的稳定和不稳定的充分条件；利用稳定性开关理论和分支理论，研究了三种不同时滞对平衡点的影响，给出了时滞变化时系统发生开关和出现Hopf分支的充分条件；最后，通过数值模拟对主要结论进行验证.
• Select
  Keller-Segel抛物系统解的爆破现象

  李远飞

  应用数学学报. 2017, 40(5): 692-701. https://doi.org/10.12387/C2017057

  摘要 ( ) PDF全文 ( )   可视化   收藏

  本文研究了Keller-Segel抛物系统在Robin边界条件下解的爆破问题.利用微分不等式技术，推导了一个一阶微分不等式，并由此不等式获得了在R³上Keller-Segel抛物系统解的爆破时间的下界.在一些适当的约束条件下，也获得了在R^N（N>3）上Keller-Segel抛物系统爆破解显式下界.
• Select
  温储备失效和单重休假Min(N,V)-策略的M/G/1可修排队系统

  蔡晓丽, 唐应辉

  应用数学学报. 2017, 40(5): 702-726. https://doi.org/10.12387/C2017058

  摘要 ( ) PDF全文 ( )   可视化   收藏

  本文考虑具有温储备失效特征和单重休假Min （N，V）-控制策略的M/G/1可修排队系统.在该系统中，服务台有两类故障：一类是服务台在服务员“广义忙期”中可能发生的故障，另一类是服务台在没有为顾客服务的时间段内可能发生的温储备故障，且假设两类故障具有不同的故障率和修复率.运用全概率分解技术、拉普拉斯变换工具以及更新过程理论，研究了系统的瞬态队长分布和稳态队长分布，获得了瞬态队长分布的拉普拉斯变换的递推表达式，得到了在系统容量的优化设计中有重要应用价值的稳态队长分布的递推结果，并证明了稳态队长的随机分解性质.同时还讨论了当休假时间V=0，V→∞与温储备寿命时间Y→∞时的特殊情形.最后，建立了系统长期单位时间内总成本费用函数，用数值计算例子讨论了最优控制策略N^*.
• Select
  关于交叉数为1的联图

  王晶, 欧阳章东, 黄元秋

  应用数学学报. 2017, 40(5): 727-733. https://doi.org/10.12387/C2017059

  摘要 ( ) PDF全文 ( )   可视化   收藏

  确定图的交叉数是NP-完全问题.Kuratowski定理刻画了平面图的特征，而结合图的交叉数这一参数来研究非平面图的特征，目前相关结果甚少.本文从联图着手，研究当G₁∨G₂的交叉数为1时，刻画出因子图G₁和G₂须满足的充要条件.
• Select
  混料试验的拟分量变换设计

  李光辉, 张崇岐

  应用数学学报. 2017, 40(5): 734-751. https://doi.org/10.12387/C2017060

  摘要 ( ) PDF全文 ( )   可视化   收藏

  在混料试验中有两类重要的设计，分别是最优设计与均匀设计.为了构造一类能兼顾最优性与均匀性的混料设计，本文在Scheffé型设计的基础上提出了混料拟分量变换设计.首先定义了填充格子点集并讨论了它的相关性质，然后以填充格子点集作为NT-net用于度量点集的均匀程度，证明了对称区域内的中心压缩拟分量变换设计最均匀，以及D-，A-最优设计的拟分量变换设计具有最优性不变的性质.通过实例分析，验证了拟分量变换设计的有效性，并且这种设计能保证在变换区域内的最优性以及整体区域的均匀性.这种方法所建立的模型与真实模型更接近，更稳健.
• Select
  有Riemann-Stieltjes积分边界条件的非线性奇异分数阶微分方程边值问题正解的存在性

  王亚平, 刘立山, 吴永洪

  应用数学学报. 2017, 40(5): 752-769. https://doi.org/10.12387/C2017061

  摘要 ( ) PDF全文 ( )   可视化   收藏

  本文主要研究下列带有Riemann-Stieltjes积分边值条件的奇异分数阶微分方程问题正解的存在性和多重性：
  

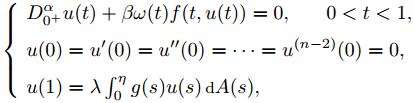
  其中β>0是参数，α>2，n-1<α≤n，0 <η≤1，0≤（λη^α）/（α）<1，函数A（s）是有界变差函数，g∈L¹[0，1]，D₀₊^α是Riemann-Liouville分数阶微分；ω：（0，1）→[0，+∞）连续，ω∈L¹（0，1）且ω（t）在t=0和t=1处奇异，非线性项f：[0，1]×（0，+∞）→[0，+∞）连续且f（t，x）在x=0处奇异.本文首先给出了该问题的Green函数及其性质，然后在一些条件下，运用Green函数的性质和不动点指数理论，并利用相关线性算子的第一特征值，得到了问题正解的存在性和多重性.接下来，以注的形式，说明了一些相关的边值问题.最后，我们给出了相关的例子，来说明我们主要结果的实用性.

• Select
  一类休假排队平稳队长的数值计算与渐近分析

  张宏波, 史定华

  应用数学学报. 2017, 40(5): 770-780. https://doi.org/10.12387/C2017062

  摘要 ( ) PDF全文 ( )   可视化   收藏

  本文讨论休假时间服从T-SPH分布的M/M/1休假排队平稳附加队长分布的数值计算以及尾部渐近特征，其中T-SPH表示可数状态吸收生灭过程吸收时间的分布.在分布PGF的基础上，得到了多重休假和单重休假两种情形平稳附加队长以及队长各阶阶乘矩的迭代公式和渐近公式，并用数值例子检验了方法的有效性.
• Select
  强混合样本情形含附加信息时总体分位数的估计

  黎玲, 李华英, 秦永松

  应用数学学报. 2017, 40(5): 781-800. https://doi.org/10.12387/C2017063

  摘要 ( ) PDF全文 ( )   可视化   收藏

  在强混合样本下，利用分组经验似然方法构造了总体分位数的一类新的估计，证明了估计的渐近正态性，同时证明了含附加信息时估计的渐近方差小于或者等于不含附加信息时估计的渐近方差.