中国科学院数学与系统科学研究院期刊网

2011年, 第34卷, 第5期　刊出日期：2011-10-27
  

  • 全选
    |
    论文
  • 单参数指数分布参数比率统计推断的研究
    李建波, 张日权
    应用数学学报. 2011, 34(5): 769-777. https://doi.org/10.12387/C2011083
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文在产品寿命服从单参数指数分布的无替换定数截尾寿命试验场合下, 提出两独立产品的平均寿命比率的两个估计量并研究了它们的均值、方差、方差的估计、大截尾数性质、置信区间及最优截尾数的确定问题. 然后进行了数据模拟, 进一步验证了所提估计量的有效性.  
  • 奇阶完备残差图
    杨世辉, 段辉明
    应用数学学报. 2011, 34(5): 778-785. https://doi.org/10.12387/C2011084
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文讨论奇阶完备残差图, 证明了对于任意奇数n, 不存在奇阶 Kn-残差图. 对任意奇数t≥3和n=2t, 2t-2,2t-4构造了一类具有奇阶2n+t的Kn-残差图. 我们证明了当n≡0, (mod 4)时, Kn-残差图的最小奇阶为(5n/2)+1; 当n≡2, (mod4)时, Kn-残差图的最小奇阶为(5n/2), 并且证明了相应的最小奇阶Kn-残差图的唯一性.  
  • 一个肿瘤侵入模型的定性分析
    张杰, 伏升茂, 崔尚斌
    应用数学学报. 2011, 34(5): 786-800. https://doi.org/10.12387/C2011085
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文研究由Gatenby和Gawlinski提出的一个肿瘤侵入模型. 该模型是一个强耦合的退缩型反应扩散方程组. 本文在 α12为零,0 ≤ α21 <1的情况下, 对该模型进行严格的数学分析. 所获结果包括 两个方面：(1) 解的整体存在性. 主要应用了逼近方法, H.Amann关于一般拟线性方程和这类方 程与常微分方程耦合而成的广义抛物型方程组解的存在性理论, 以及积分估计技术. 如何建立解的积 分估计是获得这个问题解的整体存在性的关键. (2) 解的渐近性态. 该模型有 EP1, EP2, EP3和EP4四个稳态解, 其中 EP1和 EP2两个平凡稳态解在任何情况下都不稳定. 通过构造 Lyapunov函数, 我们证明了, 在一定条件下 EP3全局渐近稳定, 从而时变解在时间趋于无穷时将趋 于 EP3, 而在相反的条件下 EP4全局渐近稳定, 从而时变解在时间趋于无穷时将趋于 EP4.  
  • 带P-Laplacian 算子的四点四阶奇异边值问题的对称正解
    栾世霞, 赵艳玲
    应用数学学报. 2011, 34(5): 801-812. https://doi.org/10.12387/C2011086
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文主要利用上下解方法和Schauder不动点定理, 在更广泛的条件下研究了一类带P-Laplacian 算子的四点四阶奇异边值问题的对称正解的存在性. 克服了对非线性微分算子[φp(u″)]″ Fredholm抉择定理和极大值原理不能使用的困难, 改进并推广了最近的一些已知结果.  
  • 一类含隅角和弯矩的奇异梁方程三个正解的存在性
    赵东霞, 王宏洲, 王军民, 赵俊芳
    应用数学学报. 2011, 34(5): 813-821. https://doi.org/10.12387/C2011087
    摘要 ( ) PDF全文 ( )   可视化   收藏
    利用格林函数方法和Avery-Peterson不动点定理研究了一类非线性四阶两点边值问题

    多个正解的存在性, 其中允许非线性项f(t,u,v,w)在t=0, t=1, u=0, v=0, w=0处奇异. 在力学上该问题模拟了左端简单支撑右端被滑动夹子夹住的弹性梁的挠曲. 由于非线性项同时涉及隅角和弯矩, 因此主要结论对于梁的稳定性分析是有益的. 最后我们给出了一个例子, 进一步证实本文理论的严密性和可行性.  
  • 希尔伯特空间中的算子样条与一类最优化方法
    张新建
    应用数学学报. 2011, 34(5): 822-829. https://doi.org/10.12387/C2011088
    摘要 ( ) PDF全文 ( )   可视化   收藏
    在抽象的Hilbert空间中讨论与线性算子和泛函有关的插值和光顺样条的表示和求解. 分析了所给算子和泛函的特征对空间结构的影响; 引入一种新的内积, 证明了新内积的完备性; 利用样条在新内积下的投影性质建立了抽象算子样条与一类最优化问题的联系; 还指出在本文的基础上可用特征值和特征向量研究抽象算子样条的构造和计算.  
  • 五点八边图的完美T(G)-三元系
    侯英涛, 康庆德, 张艳丽
    应用数学学报. 2011, 34(5): 830-837. https://doi.org/10.12387/C2011089
    摘要 ( ) PDF全文 ( )   可视化   收藏
    设G是Kn的子图. 在G的每边外添加一点,将该边扩展为一个3长圈,且所添加的点两两不同, 均异于G的诸顶点, 这样得到的图形被记为T(G). 如果3Kn的边恰好能够分拆成与T(G)同构的一些子图,则称这些子图构成一个n阶的T(G)-三元系. 进而,若此分拆的全体内部边又恰构成Kn中全部边的一个分拆,则称这个T(G)-三元系是完美的. 对于所有使得完美T(G)-三元系存在的正整数n的集合称为完美T(G)-三元系的存在谱. 对于K4的所有子图及K5的7边以下子图G,其完美T(G)-三元系的存在性问题已经在一系列文章中被完全解决. 本文将对不含孤立点的全部五点八边图G, 确定完美T(G)-三元系的存在谱.  
  • 龙虾树的多级距离标号
    侯丽霞, 左连翠
    应用数学学报. 2011, 34(5): 838-852. https://doi.org/10.12387/C2011090
    摘要 ( ) PDF全文 ( )   可视化   收藏
    连通图G的多级距离标号是指顶点集V(G)到{0,1,2,···}的一个映射f, 它使得对于任意的u,v∈V(G)满足: |f(u)-f(v)| ≥ diam(G)+1-d(u,v), 其中diam(G)是图G的直径, d(u,v)是两点u,v之间的距离. 函数f的跨度是指 . 图G的多级距离数是指它的所有多级距离标号的最小跨度. 本文研究了一类关于权中心点对称的龙虾树, 并得出了它的多级距离数的一个下界, 进而得出了它在某些特殊情况下的多级距离数的确切值.  
  • 具有中途准入机制和多重休假的离散时间GI/Geom(a,b)/1/N早到排队系统
    余妙, 唐应辉, 付永红
    应用数学学报. 2011, 34(5): 853-872. https://doi.org/10.12387/C2011091
    摘要 ( ) PDF全文 ( )   可视化   收藏
    运用补充变量方法和嵌入Markov链方法讨论了一个具有批量服务中途准入机制的离散时间多重休假排队系统.利用一种有效的数值迭代算法获得了系统中三种时刻的队长分布. 进一步, 使用不同时刻的队长分布, 通过数值化方法研究了系统参数对阻塞概率,批量服务中途准入概率, 顾客在缓冲空间中平均等待时间等几类重要性能指标的影响.  
  • 具有积分边界条件的四阶奇异特征值问题的正解
    张红侠, 刘立山, 郝新安
    应用数学学报. 2011, 34(5): 873-885. https://doi.org/10.12387/C2011092
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文研究一类具有积分边界条件的四阶奇异特征值问题正解的存在性,非线性项f(t,u) 允许在t=0和/或t=1和u=0处奇异. 首先给出一个新的比较定理, 然后构造奇异特征值问题的上下解, 最后运用Schauder不动点定理获得了当f(t,u)关于u是减的情况下正解的存在性, 给出了处理f(t,u)允许在u=0处奇异的方法, 可以处理f(t,u)在u=0 处奇异的方法并不多见.  
  • 赋范线性空间中渐近拟伪压缩型映象不动点的修改的广义Ishikawa迭代逼近
    张树义
    应用数学学报. 2011, 34(5): 886-894. https://doi.org/10.12387/C2011093
    摘要 ( ) PDF全文 ( )   可视化   收藏
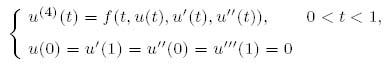
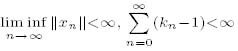    本文在去掉 条件下, 并用αn → 0(n → ∞)取代 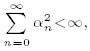, 使用新的分析技巧, 在赋范线性空间中建立了一致Lipschitz的渐近拟伪压缩型映象公共不动点的修改的广义Ishikawa迭代序列的强收敛定理, 从而本质改进和推广了唐玉超, 刘理蔚新近的结果.  
  • 偶阶半线性中立型分布时滞微分方程的振动性
    张全信, 高丽, 俞元洪
    应用数学学报. 2011, 34(5): 895-905. https://doi.org/10.12387/C2011094
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文研究偶阶半线性中立型分布时滞微分方程, 利用广义Riccati 变换和积分平均技巧得到方程一切解均为振动的若干新的振动准则, 推广和改进了一些文献中的结果.  
  • 具有两类服务中断的离散时间重试排队分析
    张冕, 侯振挺
    应用数学学报. 2011, 34(5): 906-917. https://doi.org/10.12387/C2011095
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文考虑了具有破坏性和非破坏性服务中断的离散重试排队系统.两类中断都发生在顾客接受服务的过程中, 假设服务台在工作时发生破坏性中断,则正在接受服务的顾客中断服务,进入到重试空间中去,重新尝试以接受服务; 若服务台在工作时发生非破坏性中断, 则正在接受服务的顾客将等待中断结束后再继续完成剩余的服务量.求出了系统存在稳态的充分必要条件. 利用补充变量法,求出了系统稳态时系统和重试区域中队长分布的概率母函数, 以及其他一些重要的排队指标, 并且给出了对应的连续时间下具有两类服务中断的M/G/1排队的队长分布的概率母函数. 最后, 通过数值算例研究了各种参数对平均队长的影响.  
  • 无穷维Hamilton算子的辛自伴性
    吴德玉, 阿拉坦仓
    应用数学学报. 2011, 34(5): 918-923. https://doi.org/10.12387/C2011096
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文运用算子扰动理论研究了无穷维Hamilton算子的共轭算子, 进而得到了无穷维Hamilton算子为辛自伴算子的若干充分条件.  
  • 基于次梯度选取的非光滑优化强次可行方向法
    唐春明, 简金宝
    应用数学学报. 2011, 34(5): 924-937. https://doi.org/10.12387/C2011097
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文结合次梯度选取技术及割平面法和强次可行方向法的思想, 提出了一个求解目标函数非光滑约束优化问题的强次可行方向算法.通过设计一个新的寻找搜索方向子问题和构造新型线搜索, 算法不仅能接受不可行的初始点, 而且能保持迭代点的强次可行性, 同时避免在可行域外目标函数值的不适度增加. 算法具备全局收敛性, 且初步的数值试验表明算法是稳定有效的.  
  • 双变量LMEs一种异类约束最小二乘解的MCG算法
    刘晓敏, 张凯院
    应用数学学报. 2011, 34(5): 938-948. https://doi.org/10.12387/C2011098
    摘要 ( ) PDF全文 ( )   可视化   收藏
    借鉴求线性矩阵方程组(LMEs)同类约束最小二乘解的修正共轭梯度法, 建立了求双变量LMEs的一种异类约束最小二乘解的修正共轭梯度法, 并证明了该算法的收敛性．在不考虑舍入误差的情况下, 利用该算法不仅可在有限步计算后得到LMEs的一组异类约束最小二乘解, 而且选取特殊初始矩阵时, 可求得LMEs的极小范数异类约束最小二乘解．另外, 还可求得指定矩阵在该LMEs的异类约束最小二乘解集合中的最佳逼近．算例表明, 该算法是有效的  
  • 带干扰phaes-type风险模型中的最大盈余及相关分布
    江五元
    应用数学学报. 2011, 34(5): 949-956. https://doi.org/10.12387/C2011099
    摘要 ( ) PDF全文 ( )   可视化   收藏
    本文考虑了索赔时间间距为phase-type分布时带干扰更新风险模型中的破产前最大盈余、 破产后赤字的分布, 建立了相应的积分－微分方程. 最后, 讨论了当索赔时间间距为Erlang (2)分布且索赔量满足指数分布时的特殊情形.  
在线期刊
新闻公告 更多