This paper concerns the construction and regularity of a transition (probability) function of a non-homogeneous continuous-time Markov process with given transition rates and a general state space. Motivating from a lot of restriction in applications of a transition function with continuous (in t≥0) and conservative transition rates q(t, x, Λ), we consider the case that q(t, x, Λ) are only required to satisfy a mild measurability (in t≥0) condition, which is a generalization of the continuity condition. Under the measurability condition we construct a transition function with the given transition rates, provide a necessary and sufficient condition for it to be regular, and further obtain some interesting additional results.

We consider an M^X=G=1 queueing system with two phases of heterogeneous service and Bernoulli vacation schedule which operate under a linear retrial policy. In addition, each individual customer is subject to a control admission policy upon the arrival. This model generalizes both the classical M=G=1 retrial queue with arrivals in batches and a two phase batch arrival queue with a single vacation under Bernoulli vacation schedule. We will carry out an extensive stationary analysis of the system , including existence of the stationary regime, embedded Markov chain, steady state distribution of the server state and number of customer in the retrial group, stochastic decomposition and calculation of the first moment.

Let P(G, λ) be the chromatic polynomial of a graph G. Two graphs G and H are said to be chromatically equivalent, denoted G ~ H, if P(G,λ)=P(H, λ). We write [G] = {H|H ~ G}. If [G] = {G}, then G is said to be chromatically unique. In this paper, we first characterize certain complete 6-partite graphs with 6n+1 vertices according to the number of 7-independent partitions of G. Using these results, we investigate the chromaticity of G with certain star or matching deleted. As a by-product, many new families of chromatically unique complete 6-partite graphs with certain star or matching deleted are obtained.

Receiver operating characteristic (ROC) curves are often used to study the two sample problem in medical studies. However, most data in medical studies are censored. Usually a natural estimator is based on the Kaplan-Meier estimator. In this paper we propose a smoothed estimator based on kernel techniques for the ROC curve with censored data. The large sample properties of the smoothed estimator are established. Moreover, deficiency is considered in order to compare the proposed smoothed estimator of the ROC curve with the empirical one based on Kaplan-Meier estimator. It is shown that the smoothed estimator outperforms the direct empirical estimator based on the Kaplan-Meier estimator under the criterion of deficiency. A simulation study is also conducted and a real data is analyzed.

Recurrent event data often arises in biomedical studies, and individuals within a cluster might not be independent. We propose a semiparametric additive rates model for clustered recurrent event data, wherein the covariates are assumed to add to the unspecified baseline rate. For the inference on the model parameters, estimating equation approaches are developed, and both large and finite sample properties of the proposed estimators are established.

In this paper, we discuss numerous sets of global parametric sufficient efficiency conditions under various generalized (α, η, ρ)-V-invexity assumptions for a semiinfinite multiobjective fractional programming problem.

Let X, X₁, X₂,… be a sequence of nondegenerate i.i.d. random variables with zero means, which is in the domain of attraction of the normal law. Let {a_ni, 1≤i≤n, n≥1} be an array of real numbers with some suitable conditions. In this paper, we show that a central limit theorem for self-normalized weighted sums holds. We also deduce a version of ASCLT for self-normalized weighted sums.

The loglinear model under product-multinomial sampling with constraints is considered. The asymptotic expansion and normality of the restricted minimum φ-divergence estimator (RMφDE) which is a generalization of the maximum likelihood estimator is presented. Then various statistics based on φ-divergence and RMφDE are used to test various hypothesis test problems under the model considered. These statistics contain the classical loglikelihood ratio test statistics and Pearson chi-squared test statistics. In the last section, a simulation study is implemented.

Linear mixed models (LMMs) have become an important statistical method for analyzing cluster or longitudinal data. In most cases, it is assumed that the distributions of the random effects and the errors are normal. This paper removes this restrictions and replace them by the moment conditions. We show that the least square estimators of fixed effects are consistent and asymptotically normal in general LMMs. A closed-form estimator of the covariance matrix for the random effect is constructed and its consistent is shown. Based on this, the consistent estimate for the error variance is also obtained. A simulation study and a real data analysis show that the procedure is effective.

We consider the homogeneous Cantor sets which are generalization of symmetric perfect sets, and give a formula of the exact Hausdorff measures for a class of such sets.

In this paper, the chromatic sum functions of rooted biloopless nonseparable near-triangulations on the sphere and the projective plane are studied. The chromatic sum function equations of such maps are obtained. From the chromatic sum equations of such maps, the enumerating function equations of such maps are derived. An asymptotic evaluation and some explicit expression of enumerating functions are also derived.

This paper proposes a procurement and production outsourcing model subject to a dynamic prices environment. Using the optimal control theory we obtain the necessary conditions of the optimal procurement and production policy. From the study of optimal control conditions, we derive qualitative properties of the optimal procurement and production decisions for a few exemplifying cases. Through these results we are able to provide some managerial implications for managers to make real decisions.

In this paper, dynamics of the discrete-time predator-prey system with Allee effect are investigated in detail. Conditions of the existence for flip bifurcation and Hopf bifurcation are derived by using the center manifold theorem and bifurcation theory, and then further illustrated by numerical simulations. Chaos in the sense of Marotto is proved by both analytical and numerical methods. Numerical simulations included bifurcation diagrams, Lyapunov exponents, phase portraits, fractal dimensions display new and rich dynamical behavior. More specifically, apart from stable dynamics, this paper presents the finding of chaos in the sense of Marotto together with a host of interesting phenomena connected to it. The analytic results and numerical simulations demostrates that the Allee constant plays a very important role for dynamical behavior. The dynamical behavior can move from complex instable states to stable states as the Allee constant increases (within a limited value). Combining the existing results in the current literature with the new results reported in this paper, a more complete understanding of the discrete-time predator-prey with Allee effect is given.

In this paper we study the one-dimensional reflected backward stochastic differential equations which are driven by Brownian motion as well as a mutually independent martingale appearing in a defaultable setting. Using a penalization method, we prove the existence and uniqueness of the solutions to these equations. As an application, we show that under proper assumptions the solution of the reflected equation is the value of the related mixed optimal stopping-control problem.

Let {X, X_n, n≥1} be a sequence of i.i.d.random variables with zero mean, and set S_n=X_k, EX²=σ²>0, λ(ε)=P(|S_n|≥nε). In this paper, we discuss the rate of the approximation of σ² by ε²λ(ε) under suitable conditions, and improve the corresponding results of Klesov (1994).

We study an inventory system in which products are ordered from outside to meet demands, and the cumulative demand is governed by a Brownian motion. Excessive demand is backlogged. We suppose that the shortage and holding costs associated with the inventory are given by a general convex function. The product ordering from outside incurs a linear ordering cost and a setup fee. There is a constant leadtime when placing an order. The optimal policy is established so as to minimize the discounted cost including the inventory cost and ordering cost.

EQ₁^rot nonconforming finite element approximation to a class of nonlinear dual phase lagging heat conduction equations is discussed for semi-discrete and fully-discrete schemes. By use of a special property, that is, the consistency error of this element is of order O(h²) one order higher than its interpolation error O(h), the superclose results of order O(h²) in broken H¹-norm are obtained. At the same time, the global superconvergence in broken H¹-norm is deduced by interpolation postprocessing technique. Moreover, the extrapolation result with order O(h⁴) is derived by constructing a new interpolation postprocessing operator and extrapolation scheme based on the known asymptotic expansion formulas of EQ₁^rot element. Finally, optimal error estimate is gained for a proposed fully-discrete scheme by different approaches from the previous literature.

This paper considers a perturbed renewal risk process in which the inter-claim times have a phase-type distribution under a threshold dividend strategy. Integro-differential equations with certain boundary conditions for the moment-generating function and the mth moment of the present value of all dividends until ruin are derived. Explicit expressions for the expectation of the present value of all dividends until ruin are obtained when the claim amount distribution is from the rational family. Finally, we present an example.

In this paper, we present several parametric duality results under various generalized (α,η,ρ)-V-invexity assumptions for a semiinfinite multiobjective fractional programming problem.

We analyze left-truncated and right-censored data using Cox proportional hazard models with long-term survivors. The estimators of covariate coefficients and the long-term survivor proportion are obtained by the partial likelihood method, and their asymptotic properties are also established. Simulation studies demonstrate the performance of the proposed estimators, and an application to a real dataset is provided.

Supersaturated designs (SSDs) have been widely used in factor screening experiments. The present paper aims to prove that the maximal balanced designs are a kind of special optimal SSDs under the E(f_NOD) criterion. We also propose a new method, called the complementary design method, for constructing E(f_NOD) optimal SSDs. The basic principle of this method is that for any existing E(f_NOD) optimal SSD whose E(f_NOD) value reaches its lower bound, its complementary design in the corresponding maximal balanced design is also E(f_NOD) optimal. This method applies to both symmetrical and asymmetrical (mixed-level) cases. It provides a convenient and efficient way to construct many new designs with relatively large numbers of factors. Some newly constructed designs are given as examples.

Let μ be a Radon measure on R^d which may be non-doubling. The only condition that μ must satisfy is μ(B(x, r))≤Crⁿ for all x∈R^d, r>0 and for some fixed 0<n≤d. In this paper, under this assumption, we prove that θ-type Calderón-Zygmund operator which is bounded on L²(μ) is also bounded from L¹(μ) into RBMO(μ) and from H_atb^1,∞(μ) into L¹(μ). According to the interpolation theorem introduced by Tolsa, the L^p(μ)-boundedness (1<p<1) is established for θ-type Calderón-Zygmund operators. Via a sharp maximal operator, it is shown that commutators and multilinear commutators of θ-type Calderón-Zygmund operator with RBMO(μ) function are bounded on L^p(μ) (1<p<1).

In this paper we obtain the Hölder continuity property of the solutions for a class of degenerate Schrödinger equation generated by the vector fields:
 ,
where X={X₁, ···,X_m} is a family of C^∞ vector fields satisfying the Hörmander condition, and the lower order terms belong to an appropriate Morrey type space.

In this paper, we study the regularity criteria for axisymmetric weak solutions to the MHD equa- tions in R³. Let ω_θ, J_θ and u_θ be the azimuthal component of ω, J and u in the cylindrical coordinates, respectively. Then the axisymmetric weak solution (u, b) is regular on (0, T) if (ω_θ, J_θ)∈L^q(0, T;L^q) or (ω_θ,∇(u_θe_θ))∈L^q(0, T;L^q) with 3/p+2/q≤2, 3/2<p<∞. In the endpoint case, one needs conditions (ω_θ, J_θ)∈L¹(0, T; B_∞,∞⁰) or (ω_θ,∇∇(_uθe_θ))∈L¹(0, T; B_∞,∞⁰).

In this paper, we provide a separation theorem for the singular linear quadratic (LQ) control problem of Itô-type linear systems in the case of the state being partially observable. Above all, the Kalman- Bucy filtering of the dynamics is given by means of Girsanov transformation, by which the suboptimal feedback control of the LQ problem is determined. Furthermore, it is shown that the well-posedness of the LQ problem is equivalent to the solvability of a generalized differential Riccati equation (GDRE).

Let Ω∋0 be an open bounded domain in R^N (N≥3) and 2^*(s)=2(N-s)/N-2 , 0<s<2. We consider the following elliptic system of two equations in H₀¹(Ω)×H₀¹(Ω):
,
where λ, μ>0 and α,β> 1 satisfy α+β=2^*(s). Using the Moser iteration, we prove the asymptotic behavior of solutions at the origin. In addition, by exploiting the Mountain-Pass theorem, we establish the existence of solutions.

The backward stochastic differential equations driven by both standard and fractional Brownian motions (or, in short, SFBSDE) are studied. A Wick-Itô stochastic integral for a fractional Brownian motion is adopted. The fractional Itô formula for the standard and fractional Brownian motions is provided. Introducing the concept of the quasi-conditional expectation, we study some its properties. Using the quasi-conditional expectation, we also discuss the existence and uniqueness of solutions to general SFBSDEs, where a fixed point principle is employed. Moreover, solutions to linear SFBSDEs are investigated. Finally, an explicit solution to a class of linear SFBSDEs is found.

In this paper, complex dynamics of the discrete-time predator-prey system without Allee effect are investigated in detail. Conditions of the existence for flip bifurcation and Hopf bifurcation are derived by using center manifold theorem and bifurcation theory and checked up by numerical simulations. Chaos, in the sense of Marotto, is also proved by both analytical and numerical methods. Numerical simulations included bifurcation diagrams, Lyapunov exponents, phase portraits, fractal dimensions display new and richer dynamics behaviors. More specifically, this paper presents the finding of period-one orbit, period-three orbits, and chaos in the sense of Marotto, complete period-doubling bifurcation and invariant circle leading to chaos with a great abundance period-windows, simultaneous occurrance of two different routes (invariant circle and inverse period- doubling bifurcation, and period-doubling bifurcation and inverse period-doubling bifurcation) to chaos for a given bifurcation parameter, period doubling bifurcation with period-three orbits to chaos, suddenly appearing or disappearing chaos, different kind of interior crisis, nice chaotic attractors, coexisting (2,3,4) chaotic sets, non-attracting chaotic set, and so on, in the discrete-time predator-prey system. Combining the existing results in the current literature with the new results reported in this paper, a more complete understanding is given of the discrete-time predator-prey systems with Allee effect and without Allee effect.

We describe an approach to studying the center problem and local bifurcations of critical periods at infinity for a class of differential systems. We then solve the problem and investigate the bifurcations for a class of rational differential systems with a cubic polynomial as its numerator.

In this study, we consider the Bayesian estimation of unknown parameters and reliability function of the generalized exponential distribution based on progressive Type-Ⅰ interval censoring. The Bayesian estimates of parameters and reliability function cannot be obtained as explicit forms by applying squared error loss and Linex loss functions, respectively; thus, we present the Lindley's approximation to discuss these estimations. Then, the Bayesian estimates are compared with the maximum likelihood estimates by using the Monte Carlo simulations.

Quasi-Wilson nonconforming finite element approximation for a class of nonlinear Sobolev equations is discussed on rectangular meshes. We first prove that this element has two special characters by novel approaches. One is that (∇_h(u-I_hu),∇h^vh)h may be estimated as order O(h²) when u∈h³(Ω), where I_hu denotes the bilinear interpolation of u, v_h is a polynomial belongs to quasi-Wilson finite element space and ∇h denotes the piecewise defined gradient operator, h is the mesh size tending to zero. The other is that the consistency error of this element is of order O(h²)/O(h³) in broken H¹-norm, which is one/two order higher than its interpolation error when u∈H³(Ω)/H⁴(Ω). Then we derive the optimal order error estimate and su- perclose property via mean-value method and the known high accuracy result of bilinear element. Furthermore, we deduce the global superconvergence through interpolation post processing technique. At last, an extrapolation result of order O(H³), two order higher than traditional error estimate, is obtained by constructing a new suitable extrapolation scheme.

Let B_R be the ball centered at the origin with radius R in R^N (N≥2). In this paper we study the existence of solution for the following elliptic system
 
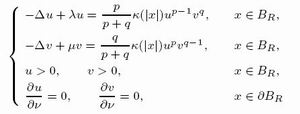
where λ>0, μ>0 p≥2, q≥2, υ is the unit outward normal at the boundary ∂BR. Under certain assumptions on κ(|x|), using variational methods, we prove the existence of a positive and radially increasing solution for this problem without growth conditions on the nonlinearity.

A system of delay differential equations is studied which represent a model for four neurons with time delayed connections between the neurons and time delayed feedback from each neuron to itself. The linear stability and bifurcation of the system are studied in a parameter space consisting of the sum of the time delays between the elements and the product of the strengths of the connections between the elements. Meanwhile, the bifurcation set are drawn in the parameter space.

The convergence to steady state solutions of the Euler equations for weighted compact nonlinear schemes (WCNS) [Deng X. and Zhang H. (2000), J. Comput. Phys. 165, 22-44 and Zhang S., Jiang S. and Shu C.-W. (2008), J. Comput. Phys. 227, 7294-7321] is studied through numerical tests. Like most other shock capturing schemes, WCNS also suffers from the problem that the residue can not settle down to machine zero for the computation of the steady state solution which contains shock waves but hangs at the truncation error level. In this paper, the techniques studied in [Zhang S. and Shu. C.-W. (2007), J. Sci. Comput. 31, 273-305 and Zhang S., Jiang S and Shu. C.-W. (2011), J. Sci. Comput. 47, 216-238], to improve the convergence to steady state solutions for WENO schemes, are generalized to the WCNS. Detailed numerical studies in one and two dimensional cases are performed. Numerical tests demonstrate the effectiveness of these techniques when applied to WCNS. The residue of various order WCNS can settle down to machine zero for typical cases while the small post-shock oscillations can be removed.

We study the semi-classical limit of the Schrödinger equation in a crystal in the presence of an external potential and magnetic field. We first introduce the Bloch-Wigner transform and derive the asymptotic equations governing this transform in the semi-classical setting. For the second part, we focus on the appearance of the Berry curvature terms in the asymptotic equations. These terms play a crucial role in many important physical phenomena such as the quantum Hall effect. We give a simple derivation of these terms in different settings using asymptotic analysis.

This paper is concerned with the estimating problem of a semiparametric varying-coefficient partially linear errors-in-variables model Y_i = X_i^τ +Z_i^τ (U_i)+ε_i, W_i = X_i+ ξ_i, i = 1,…, n. Due to measurement errors, the usual profile least square estimator of the parametric component, local polynomial estimator of the nonparametric component and profile least squares based estimator of the error variance are biased and inconsistent. By taking the measurement errors into account we propose a generalized profile least squares estimator for the parametric component and show it is consistent and asymptotically normal. Correspondingly, the consistent estimation of the nonparametric component and error variance are proposed as well. These results may be used to make asymptotically valid statistical inferences. Some simulation studies are conducted to illustrate the finite sample performance of these proposed estimations.

In this paper, we present a new trust region algorithm for a nonlinear bilevel programming problem by solving a series of its linear or quadratic approximation subproblems. For the nonlinear bilevel programming problem in which the lower level programming problem is a strongly convex programming problem with linear constraints, we show that each accumulation point of the iterative sequence produced by this algorithm is a stationary point of the bilevel programming problem.

The flow on theWiener space associated to a tangent process constructed by Cipriano and Cruzeiro, as well as by Gong and Zhang does not allow to recover Driver’s Cameron-Martin theorem on Riemannian path space. The purpose of this work is to refine the method of the modified Picard iteration used in the previous work by Gong and Zhang and to try to recapture and extend the result of Driver. In this paper, we establish the existence and uniqueness of a flow associated to a Cameron-Martin type vector field on the path space over a Riemannian manifold.

In this paper the large time behavior of the global L^∞ entropy solutions to the hyperbolic system with dissipative structure is investigated. It is proved that as t→∞ the entropy solutions tend to a constant equilibrium state in L² norm with exponential decay even when the initial values are arbitrarily large. As an illustration, a class of 2×2 system is studied.

The spectral spread of a graph is defined to be the difference between the largest and the least eigenvalue of the adjacency matrix of the graph. A graph G is said to be bicyclic, if G is connected and |E(G)| = |V(G)| + 1. Let B(n, g) be the set of bicyclic graphs on n vertices with girth g. In this paper some properties about the least eigenvalues of graphs are given, by which the unique graph with maximal spectral spread in B(n, g) is determined.