Mieczysław Cichoń, Hussein A.H. Salem
In this paper we investigate the existence of solutions of the nonhomogeneous three-point boundary value problem
The coefficient functions
a and
b are continuous real-valued functions on [0, 1],
η and
ζ are some positive constants. Denote by
E a Banach space and assume, that u belongs to an Orlicz space i.e.,
u(·)∈
LM([0, 1],R), where M is an N-function and
c∈
E.
We search for solutions of the above problem in the Banach space of continuous functions
C([0, 1],
E) with the Pettis integrability assumptions imposed on
f. Some classes of Pettis-integrable functions are described in the paper and exploited in the proofs of main results. We stress on a class of pseudo-solutions of considered problem. Our results extend previous results of the same type for both Bochner and Pettis integrability settings. Similar results are also proved for differential inclusions i.e. when
f is a multivalued function.
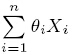and their maxima. In this paper, we generalize their work to the situation that {Xi, i≥1} is a sequence of upper tail asymptotically independent random variables with common distribution from the class D∩L, and {θi, i≥1} is a sequence of nonnegative random variables, independent of {Xi,i≥1} and satisfying some regular conditions. Moreover, no additional assumption is required on the dependence structure of {θi, i≥1}.
